four.4 Measures of central tendency
4.4.3 Calculating the mode

Text begins

When it'south unique, the mode is the value that appears the about often in a data gear up and information technology can exist used as a mensurate of central tendency, like the median and mean. Simply sometimes, at that place is no manner or there is more than one mode.

There is no mode when all observed values announced the same number of times in a data ready. There is more than one mode when the highest frequency was observed for more than one value in a data set. In both of these cases, the mode can't be used to locate the centre of the distribution.

The mode tin exist used to summarize chiselled variables, while the hateful and median can be calculated only for numeric variables. This is the chief reward of the mode as a measure of central tendency. Information technology's as well useful for discrete variables and for continuous variables when they are expressed as intervals.

Here are some examples of adding of the way for discrete variables.

Example 1 – Number of points during a hockey tournament

During a hockey tournament, Audrey scored 7, v, 0, 7, 8, 5, 5, 4, 1 and 5 points in ten games. After summarizing the data in a frequency table, you can easily see that the mode is 5 because this value appears the most oftentimes in the data set (4 times). The way can be considered a mensurate of key tendency for this data set because information technology's unique.



Table four.4.three.1
Number of games past the number of points scored
Table summary
This table displays the results of Number of games by the number of points scored. The information is grouped past Number of points scored (appearing equally row headers), Frequency (number of games) (appearing as column headers).
Number of points scored Frequency (number of games)
0   1
1   1
4   one
5   iv
seven   ii
viii   ane
0 true nil or a value rounded to zero

Case 2 – Number of points in 12 basketball games

During Marco's 12-game basketball flavour, he scored fourteen, 14, 15, 16, 14, 16, 16, eighteen, fourteen, 16, 16 and fourteen points. After summarizing the data in a frequency tabular array, you can see that there are two modes in this data set: 14 and 16. Both values appear five times in the information set up and 5 is the highest frequency observed. The fashion tin't be used a measure of central tendency because there is more one mode. It's a bimodal distribution.



Tabular array 4.4.3.ii
Number of games past the number of points scored
Table summary
This table displays the results of Number of games past the number of points scored. The information is grouped by Number of points scored (appearing equally row headers), Frequency (number of games) (appearing as column headers).
Number of points scored Frequency (number of games)
xiv 5
15 1
xvi five
18 i

Example 3 – Number of touchdowns scored during football season

The following information set up represents the number of touchdowns scored past Jerome in his high-school football season: 0, 0, 1, 0, 0, 2, 3, one, 0, i, 2, three, one, 0. Let'due south compare the mean, median and mode.
The sum of all values is 14 and there are 14 data points. This gives a mean of 1. Because the number of values is fifty-fifty, the median is average between the data betoken of rank 7 and the data point of rank 8, afterwards arranging the data ready in increasing social club.



Table 4.iv.3.3
Rank associated with each value of the number of touchdowns during football flavour
Tabular array summary
This table displays the results of Rank associated with each value of the number of touchdowns during football season. The data is grouped by Rank (appearing as row headers), Number of touchdowns (appearing as column headers).
Rank Number of touchdowns
1 0
2 0
3 0
4 0
five 0
half dozen 1
7 ane
8 ane
9 1
10 ane
11 2
12 two
13 3
14 3

Therefore, the median is equal to 1. Once the information has been summarized in a frequency tabular array, you tin see that the mode is 0 because it is the value that appears the most often (vi times).



Tabular array 4.iv.iii.4
Number of games past the number of touchdowns
Table summary
This table displays the results of Number of games by the number of touchdowns. The information is grouped past Number of touchdowns (appearing as row headers), Frequency (appearing as column headers).
Number of touchdowns Frequency
0 6
one 4
two 2
3 ii
0 true aught or a value rounded to zero

In summary, in this case, the mean is i, the median is one and the mode is 0.

The mode is not used equally much for continuous variables considering with this type of variable, it is likely that no value will appear more than once. For example, if you ask xx people their personal income in the previous year, it'south possible that many will have amounts of income that are very close, but that you lot will never get exactly the same value for two people. In such example, it is useful to group the values in mutually sectional intervals and to visualize the results with a histogram to place the modal-class interval.

Case 4 – Height of people in the arena during a basketball game

Nosotros are interested in the superlative of the people nowadays in the arena during a basketball game game. Table 4.4.3.5 presents the number of people for 20-centimetre intervals of acme.



Tabular array 4.iv.iii.5
Number of people by pinnacle intervals
Table summary
This tabular array displays the results of Number of people by superlative intervals. The information is grouped by Height (in centimetres) (actualization as row headers), Frequency (number of people) (appearing as column headers).
Peak (in centimetres) Frequency (number of people)
20 to 39 42
40 to 59 105
60 to 79 176
80 to 99 230
100 to 119 214
120 to 139 168
140 to 159 363
160 to 179 480
180 to 200 170
200 to 219 11

Chart 4.4.3.1 shows this data set as a histogram.

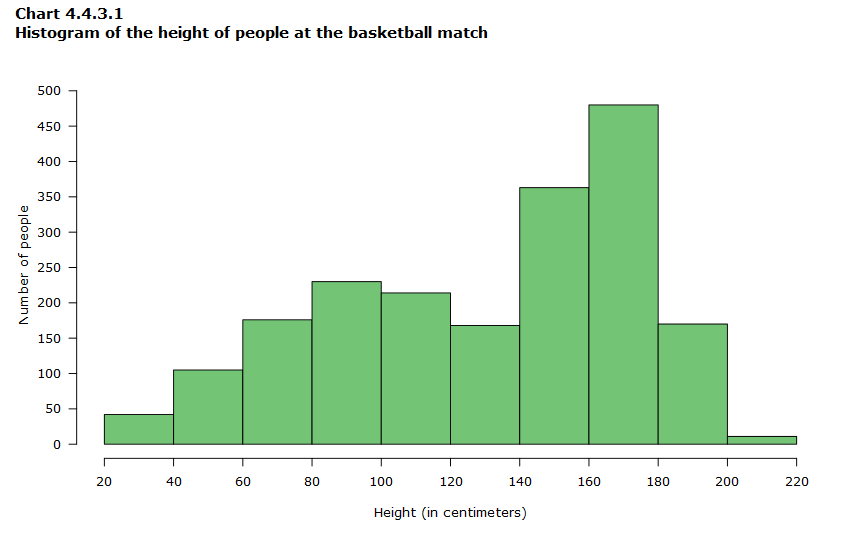
Chart 4.4.3.1 Histogram of the height of people at the basketball match

Information table for Nautical chart 4.iv.iii.one

Data illustrated in this chart are the data from table 4.4.3.5.

Looking at the table and histogram, y'all can hands place the modal-class interval, 160 to 179 centimetres, whose frequency is 480. You can also see that as the height decreases from this interval, the frequency too decreases for the interval 140 to 159 centimetres (363) and it continues to decrease for 120 to 139 centimetres (168), before starting to increment until the height reaches 80 to 99 centimetres (230).

For chiselled or discrete variables, multiple modes are values that reach the same frequency: the highest ane observed. For continuous variables, all peaks of the distribution can exist considered modes even if they don't have the same frequency. The distribution for this example is bimodal, with a major fashion corresponding to the modal-class interval 160 to 179 centimetres and a minor style respective to the modal-grade interval 80 to 99 centimetres. The modal class shouldn't be used every bit a measure of cardinal tendency, simply finding two modes gives us an indication that there could exist two distinct groups in the information that should be analyzed separately.


Report a trouble on this page

Is something non working? Is at that place information outdated? Tin't find what you're looking for?

Please contact us and allow the states know how we can help you.

Privacy notice

Date modified: